model_since 1959.
model_from :

nav_classification
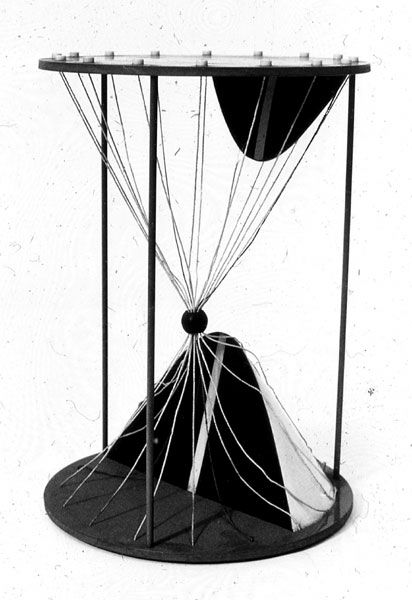
Hyperbolic section of a right circular cone
The model shows the intersection of a plane with a rotary cone. Because the intersection angle between the the plane and the axis of the rotary cone is smaller than the opening angle of the cone, the intersection figure is a "hyperbola"
The two lines, in which the plane parallel to the plane of the hyperbola through the apex of the cone intersects the surface of the cone, are marked in the model.
The intersection between a plane and circular cone (second-order cone) is always a curve of the second order. Multiple figures, that can have a conic section, of this model series are going through a rotary cone: ellipse, paraboloid and hyperbola. The appearance of the conic section depends on the angle between the intersection curve and the rotation axis, in relation to the opening angle of the rotary cone, which is the angle between the surface lines and the rotation axis.
The conic sections can degenerate into pairs of straights, if the intersection is lead through the apex of the cone. Depending on the intersection angle the straight is imaginary (degenerated ellipse, only the apex is a real part of the intersection figure), collapsed (degenerated parabola) or real (degenerated hyperbola).